As someone who’s been intrigued by how math influences the world around us, I find it fascinating how essential complex financial formulas are in making decisions, managing risks, and even forecasting the future. If you’re like me, you might have wondered how the financial world relies on intricate formulas to keep things in check. Today, I want to take you through 10 of the most complex mathematical formulas that play a significant role in finance – but don’t worry, I’ll break them down as simply as possible with examples!
Table of Contents
1. Black-Scholes Model (Option Pricing Formula)
The Black-Scholes formula is used to determine the price of European-style options. It helps investors know the price they should pay for an option by estimating future market movements.
Formula:
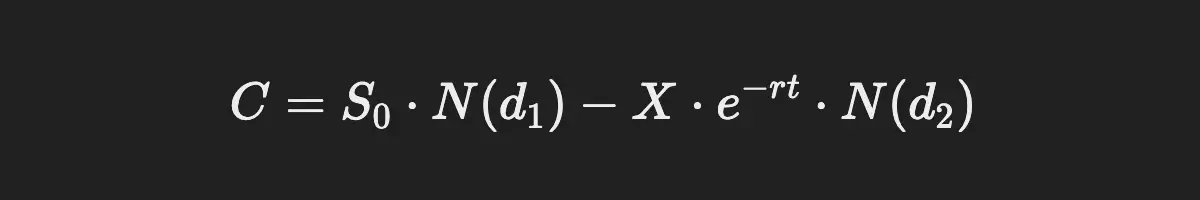
Where:
- C = Call option price
- S0 = Current stock price
- X = Strike price of the option
- t = Time to maturity
- r = Risk-free interest rate
- N(d1) and N(d2) = Cumulative distribution functions of a standard normal distribution.
Example: Imagine a stock is priced at $100, the strike price is $95, and there are 6 months to expiry. Using the Black-Scholes model, we would input these values into the formula to find out the fair value of the call option. Let’s assume the calculated price is $8.00.
2. Time Value of Money (TVM)
The concept of TVM asserts that money available today is worth more than the same amount in the future, due to its earning potential. The key formula for future value (FV) is:
Formula:
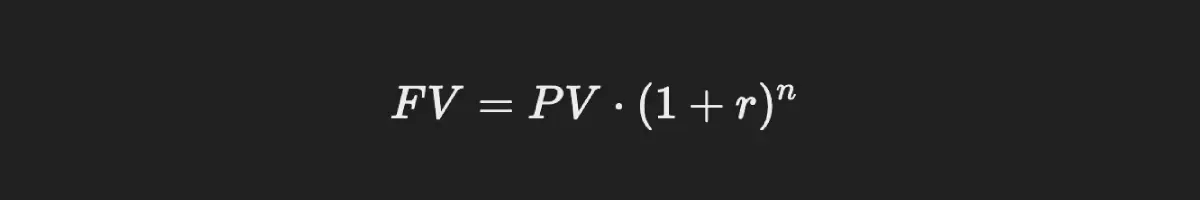
Where:
- PV = Present value
- r = Interest rate
- n = Number of periods
Example: If you invest $1,000 today at an interest rate of 5% per year for 10 years, your future value will be:
FV = 1000⋅(1+0.05)10 = 1628.89
3. Net Present Value (NPV)
NPV helps in evaluating the profitability of an investment or project. It’s the difference between the present value of cash inflows and outflows over a period.
Formula:
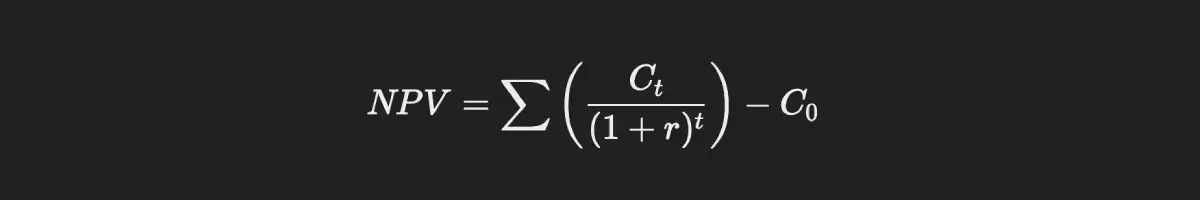
Where:
- Ct = Cash flow at time t
- r = Discount rate
- C0 = Initial investment
Example: You invest $10,000 today, and expect to receive $3,000 each year for 5 years at a discount rate of 7%. The NPV would be calculated as the sum of each year’s discounted cash flow, minus the initial investment. If NPV is positive, the investment is profitable.
4. Internal Rate of Return (IRR)
IRR is the rate at which the NPV of all cash flows from a project equals zero. It’s often used in budgeting and project evaluation.
Formula:
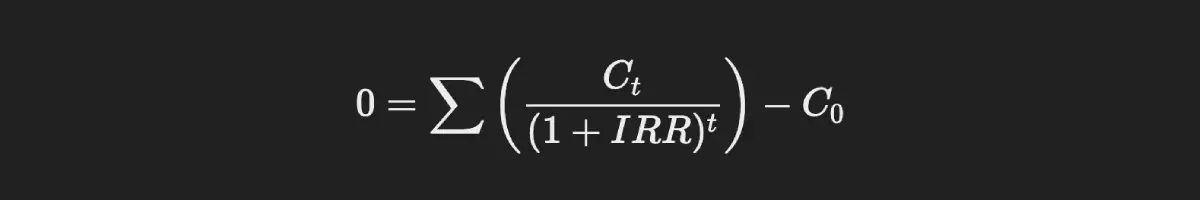
Example: Suppose you invested $5,000, and you receive $1,200 every year for 6 years. The IRR will be the rate that makes the sum of discounted cash inflows equal to the initial investment. A common IRR might be around 8%.
5. Compound Interest Formula
Compound interest is the interest on a loan or deposit, calculated based on both the initial principal and the accumulated interest.
Formula:
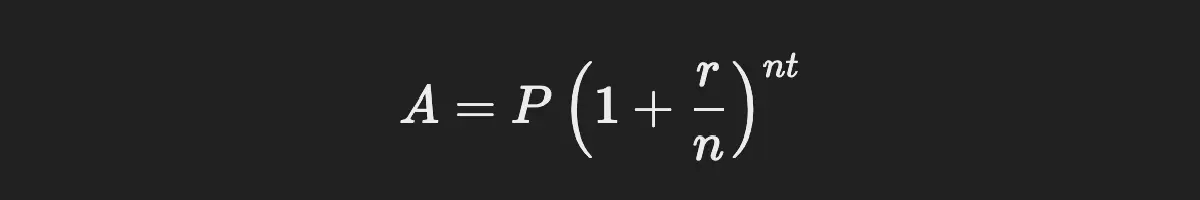
Where:
- A = Amount of money accumulated after nnn years, including interest.
- P = Principal amount.
- r = Annual interest rate.
- n = Number of times interest is compounded per year.
- t = Time in years.
Example: If you invest $2,000 at an interest rate of 4%, compounded quarterly for 5 years:
A = 2000(1+0.044)4⋅5 = 2449.48
6. Capital Asset Pricing Model (CAPM)
CAPM describes the relationship between expected return and risk of investing in a security. It helps to price risky securities and determine expected returns.
Formula:
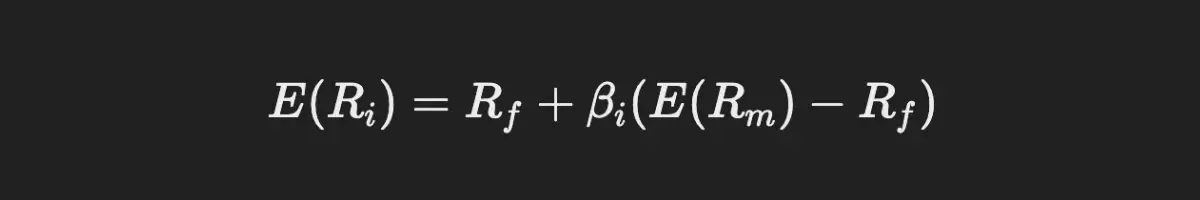
Where:
- E(Ri) = Expected return of the investment.
- Rf = Risk-free rate.
- βi = Beta of the investment.
- E(Rm) = Expected return of the market.
Example: If the risk-free rate is 2%, the market return is expected to be 7%, and a stock has a beta of 1.2, then the expected return is:
E(Ri) = 2%+1.2(7%−2%) = 8%
7. Bond Pricing Formula
The price of a bond is the present value of its future coupon payments and face value.
Formula:
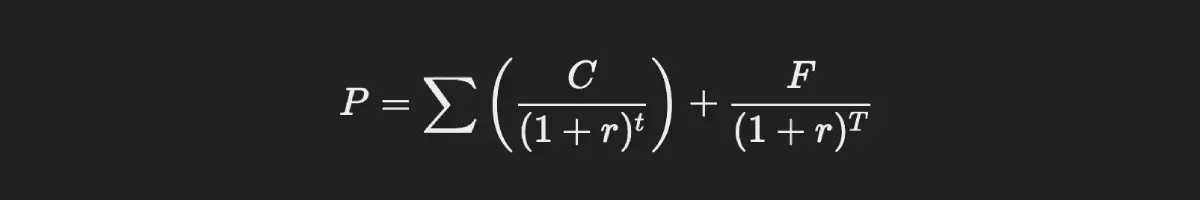
Where:
- P = Price of the bond.
- C = Coupon payment.
- F = Face value of the bond.
- r = Discount rate.
- t = Time period.
Example: If a bond pays $50 annually in coupons, has a face value of $1,000, and a discount rate of 5%, then the price can be calculated accordingly.
8. Sharpe Ratio (Financial Formulas)
The Sharpe ratio measures the performance of an investment compared to a risk-free asset, after adjusting for its risk.
Formula:
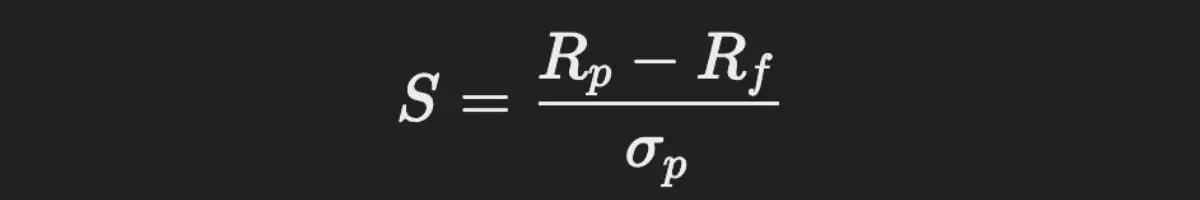
Where:
- Rp = Return of the portfolio.
- Rf = Risk-free rate.
- σp = Standard deviation of the portfolio’s excess return.
Example: If your portfolio has a return of 12%, the risk-free rate is 2%, and the standard deviation is 10%, the Sharpe ratio would be:
S = (12%−2%) / 10% = 1
9. Debt-to-Equity Ratio
This ratio helps assess a company’s financial leverage by comparing its total liabilities to its shareholder equity.
Formula:
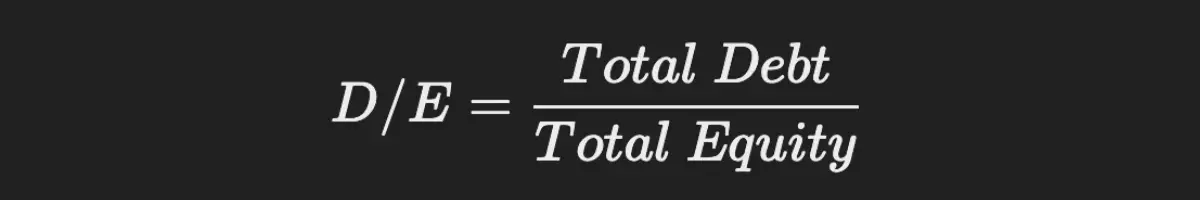
Example: If a company has $200,000 in debt and $400,000 in equity, the debt-to-equity ratio would be:
D/E = 200,000 / 400,000 = 0.5
10. Payback Period
The payback period helps investors determine how long it will take to recoup their initial investment.
Formula:
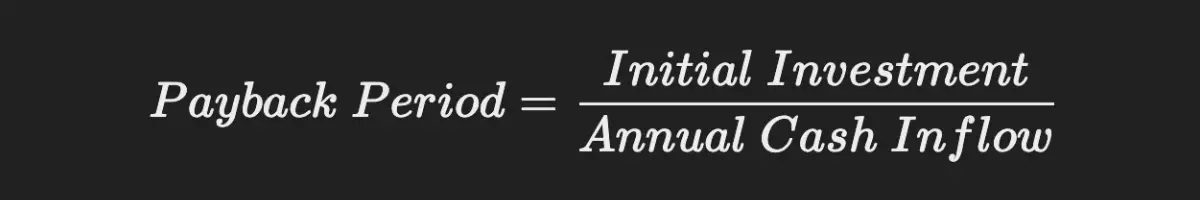
Example: If you invest $10,000 and receive $2,500 per year, the payback period will be:
10,000 / 2,500 = 4 years
Conclusion

While these formulas might seem complex at first, they play a pivotal role in the finance world. Whether you’re an investor or a curious individual like me, understanding these formulas gives a deeper insight into how financial decisions are made. And the more you practice applying them, the easier they become! Comment below if you also need a excel or google sheet of these financial formulas, I’ll be happy to provide it here!



